做一个有温度和有干货的技术分享作者 —— Qborfy

今天我们来学习 激活函数​

一句话核心：激活函数(Rectification Function): 在神经网络模型里，如何把“激活的神经元的特征”通过函数把特征保留并映射出来， 通常f(x) = wx + b中 f就是激活函数。

也简单理解成神经网络的 “智能开关”​。

是什么？

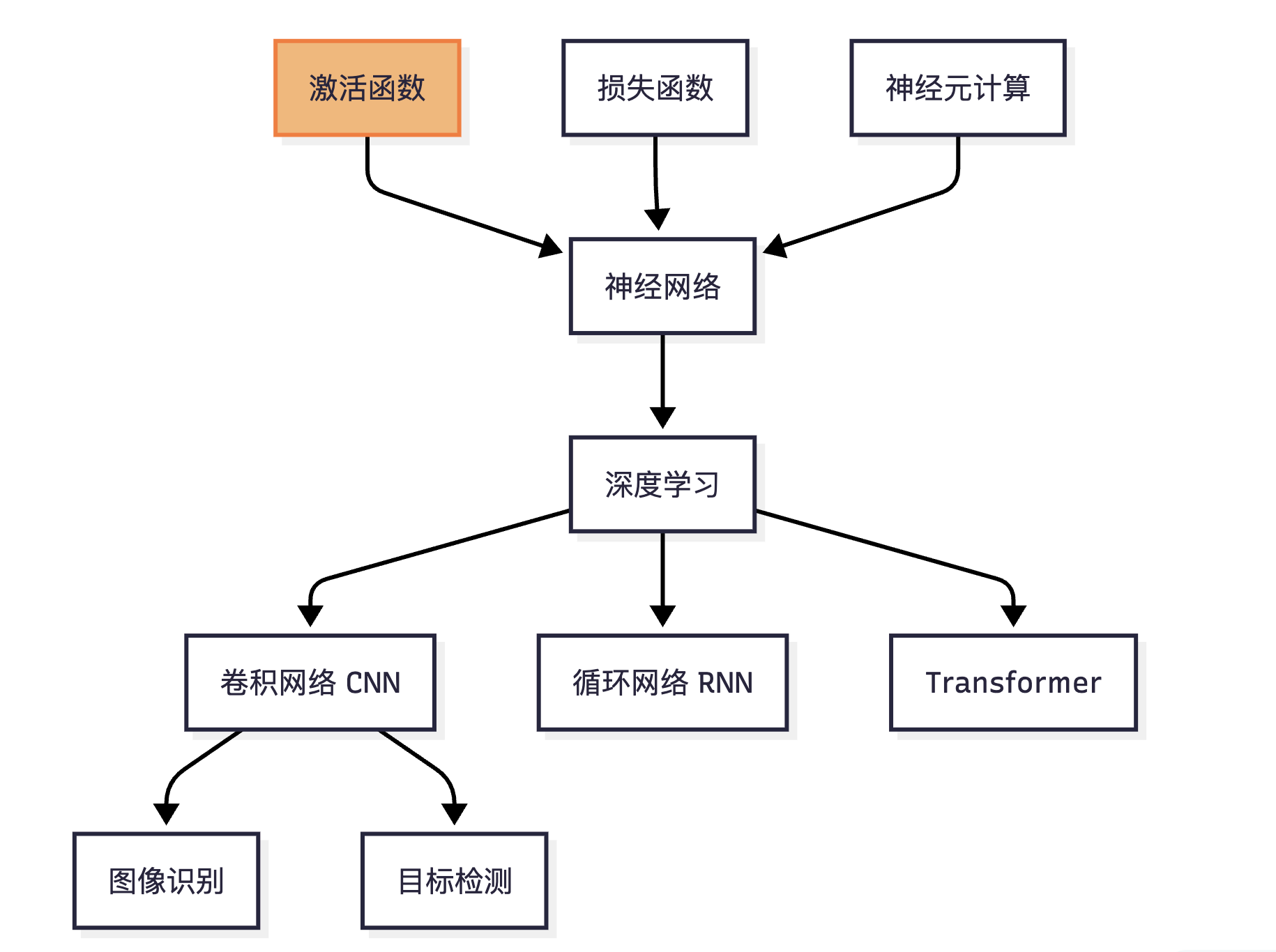
百科定义: 激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

三大核心功能​​：

​- ​引入非线性​​：使网络能够拟合任意复杂函数（否则多层网络≈单层线性模型）

• 数学表达：Output=f(∑wi*xi+b)
  ​- ​特征过滤​​：抑制噪声信号，保留有效特征（如ReLU过滤负值）
• ​​梯度调控​​：控制反向传播时的参数更新强度（防梯度消失/爆炸）

可以理解：大脑神经元 → 超过阈值才放电 → 激活函数决定信号是否向下传递

怎么做

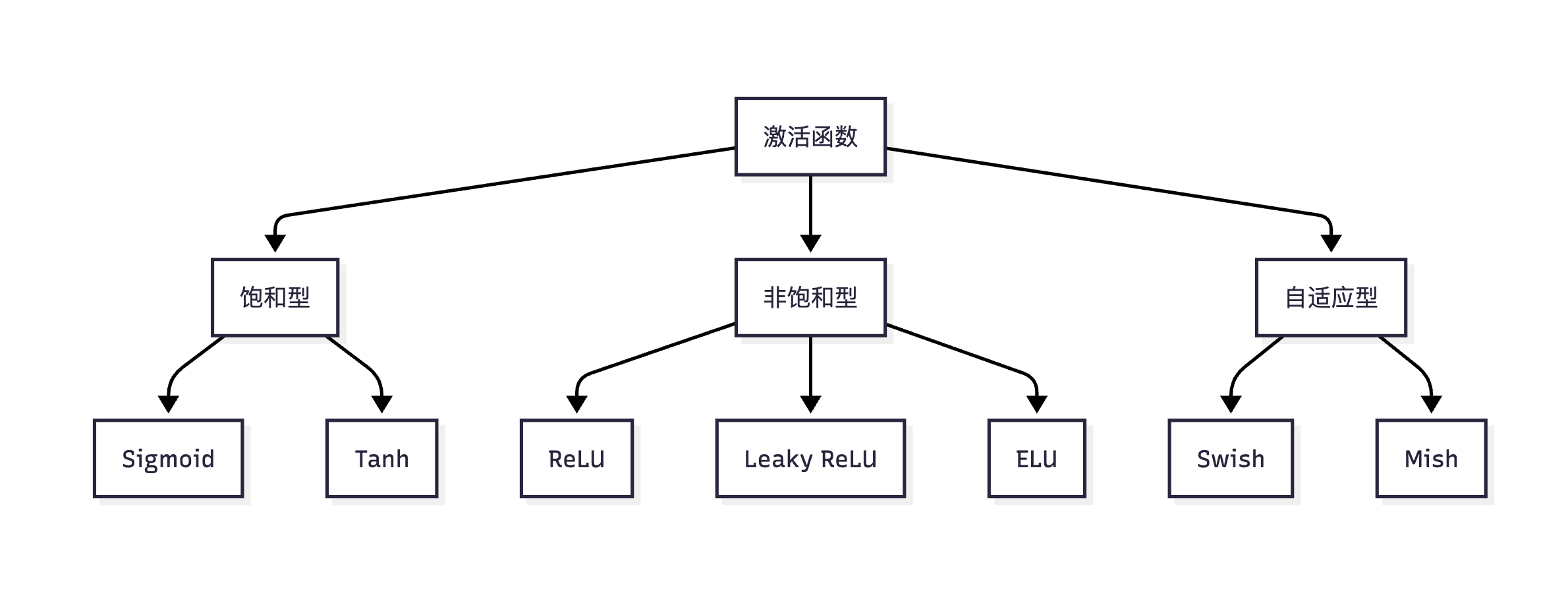
目前有 5 个经典主流激活函数：

1. Sigmoid（逻辑函数）​：​f(x) = 1/(1+e^(-x))，输出(0,1)范围，适用二分类输出层（如信用风险预测），存在梯度问题（梯度消失/爆炸）
2. ​​Tanh（双曲正切）​：​f(x) = (e^x - e^(-x))/(e^x + e^(-x))，输出(-1,1)范围，RNN/LSTM隐藏层（时序数据建模），梯度消失问题仍存在
3. ReLU（修正线性单元）​：f(x) = max(0,x)，输出[0,∞)范围，CNN/Transformer隐藏层（90%现代网络首选），解决梯度消失问题，但是存在Dead ReLU（负输入永久失活）
4. ​​Leaky ReLU（带泄露修正）​：f(x) = max(0.01x,x)，输出[0,∞)范围，解决Dead ReLU问题，但存在梯度消失问题，解决Dead ReLU → 负数区保留微小梯度
5. ​​Swish（自门控函数）​：f(x) = x * σ(βx)，Google Brain提出，β可学习，超越ReLU的基准精度，主要作用在移动端高效模型（MobileNetV3）

理解梯度和梯度问题？

梯度：反向传播时，参数更新的方向和大小。

梯度问题：在模型训练的时候，接受反向传播时，如果梯度值很小，那么参数更新就会很慢，甚至无法更新，导致训练过程无法收敛，最终无法得出正确的特征。

函数性能对比表

动手实验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 激活函数效果可视化工具
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-5, 5, 100)
functions = {
    'Sigmoid': lambda x: 1/(1+np.exp(-x)),
    'Tanh': np.tanh,
    'ReLU': lambda x: np.maximum(0, x),
    'Swish': lambda x: x/(1+np.exp(-x))
}

plt.figure(figsize=(10,6))
for name, func in functions.items():
    plt.plot(x, func(x), label=name, lw=3)
plt.legend()
plt.show()

观察重点：

• Sigmoid/Tanh的饱和区（两端平坦） → 梯度消失根源
• ReLU的负数截断 → Dead ReLU问题可视化

冷知识

1. 神经元激活率实验：

   • Sigmoid网络仅3-5%神经元激活 → 效率低下
   • ReLU网络激活率可达50% → 资源高效利用

2. 生物化学启发：
   Swish函数的平滑性灵感源于 神经突触的离子通道动力学

3. 谷歌的自动搜索：
   用强化学习在10万种函数中发现 Swish ($x \cdot \sigma(x)$) 超越人类设计

4. 宇宙学级应用：
   欧洲核子研究中心(CERN)用 GELU函数（高斯误差线性单元）处理粒子碰撞数据，误差降低38%

赏

谢谢你请我吃糖果

支付宝

微信